練習問題
問1.流体が規則的に揃い流れる状態を何というか。
解答:層流
問2.流体が複雑に混じり合いながら、不規則な渦運動をする流れの状態を何というか。
解答:乱流
問3.層流における最大流量umaxと平均流量uの関係を答えよ。
解答:![]()
問4.F:摩擦による流れのエネルギー損失、f:摩擦係数、u:流体の平均速度[m/s]、L:配管長さ[m]、D:管の内径[m]としてファニングの式を答えよ。
解答:
問5.連続の式について記述せよ。
解答:「定常流れにおいて、流体の質量流量は流線上のどの断面でも常に一定である」という法則
問6.ベルヌーイの定理について記述せよ。
解答:「理想流体の定常流れにおいて、流線上でエネルギーが保存される」ことを示した定理です。
演習問題
次の各問いに対して正しいかどうか答えなさい。また、誤っている場合、誤りの部分を正しく直しなさい。
問1.円管内の流速を上げていくと、流れの状態は層流から乱流になっていく。
解答:正しい
解説:円管内の流れは、流速の増加とともに、次第に層流→乱流になります。
問2.乱流では流体の各部が管壁に平行に流れ、 層流では流れの各部が不規則な方向に互いに入り乱れながら流れる。
解答:誤り 乱流 → 層流 and 乱流 → 層流
解説:一般に層流は規則的な流れ、乱流は不規則的な流れです。
問3.一般的に、流体輸送は乱流域で行われるため、油や高分子溶液など粘度の高い液体では、乱流状態で輸送されることが多い。
解答:誤り 乱流 → 層流
解説:粘度が高くなると、レイノルズ数は分母が大きくなるため、層流になります。
問4.レイノルズ数が5,000である流れは層流である
解答:誤り 層流 → 乱流
解説:Re(レイノルズ数)>4,000であれば乱流、2,100<Re(レイノルズ数)であれば層流となります。
問5.レイノルズ数が3,000のときは、流れは層流である
解答:誤り 層流 → 遷移域
解説:2,100<Re<4,000の間は遷移域といい、乱流と層流が混ざった状態となります。
問6.レイノルズ数は、管の内径、流体の平均流速、動粘性係数を用いて求められる。
解答:正しい
解説:レイノルズ数は次の式で表されます。![]()
Re :レイノルズ数[無次元]、D:管の内径[m]、U:平均的な流速[m/s]、ν =η/ρ:動粘性係数[m2/s]、η:流体の粘性係数[kg/m・s]
問7.レイノルズ数を求めることで乱流や層流など、 流れの状態がおおよそ把握できる。
解答:正しい
解説:レイノルズ数は流れの状態を把握できる無次元数です。
問8.流れの状態が乱流の場合、 同一管における平均流速が3倍になると、圧力損失はおよそ9倍になる。
解答:正しい
解説:乱流における圧力損失は次のファニングの式で表されます。
ファニングの式:![]()
ΔP:摩擦によりエネルギー損失[J/kg]、ρ:密度[kg/m3]、u:管内の平均流量[m/s]
L:管の長さ[m]、D:管の内径[m]
問9.円管内を流れる流体の摩擦によるエネルギー損失は、 層流ではファニングの式で求められる。
解答:誤り 層流 → 乱流 or ファニングの式 → ハーゲン・ポアズイユの式
解説:乱流における摩擦エネルギー損失は次のファニングの式で表されます。
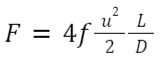
問10.円管内の流れが乱流で管摩擦係数が一定のとき、 摩擦による圧力損失は平均速度の二乗に比例し、 管の長さに無関係である。
解答:誤り 無関係である。 → 関係する。 or 比例する。
解説:乱流における摩擦のエネルギー損失は次式で表されるため、管の長さに比例します。
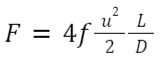
F:摩擦によりエネルギー損失[J/kg]、f:管摩擦係数、u:管内の平均流量[m/s]
L:管の長さ[m]、D:管の内径[m]
問11.乱流では、管内壁面が粗くなると摩擦のエネルギー損失は小さくなる。
解答:誤り 小さくなる → 大きくなる
解説:管内壁面が粗くなると管摩擦係数が大きくなります。管摩擦係数が大きくなると次式で表されるファニングの式から摩擦のエネルギー損失は大きくなります。
F:摩擦によりエネルギー損失[J/kg]、f:管摩擦係数、u:管内の平均流量[m/s]、
L:管の長さ[m]、D:管の内径[m]
問12.流れによるエネルギーの損失は、管路断面が急激に縮小したり拡大する場合にも起こる。
解答:誤り には起こらない → にも起こる。
解説:流れによるエネルギー損失は、管路断面の大きさが変わると起こります。



コメント